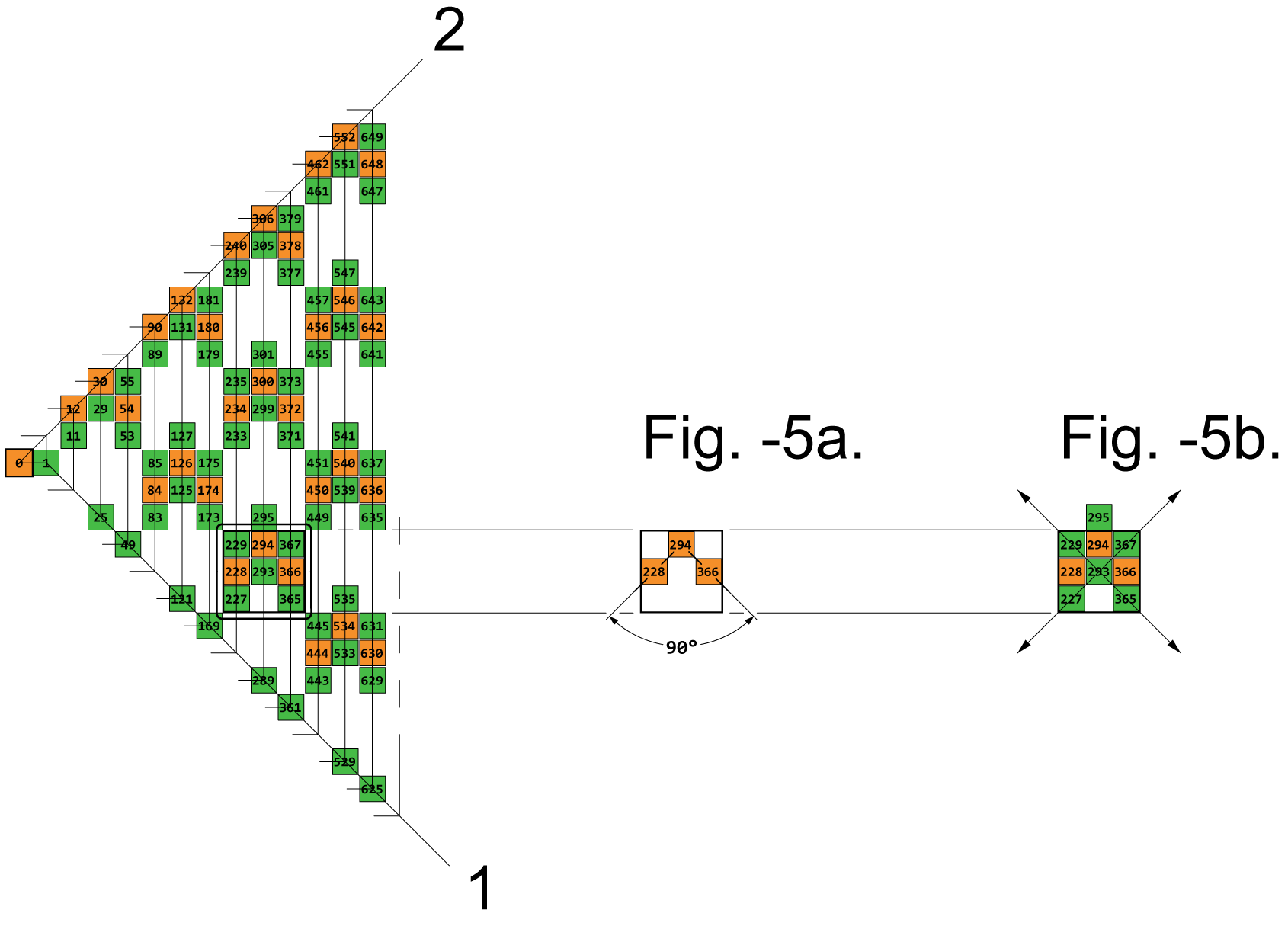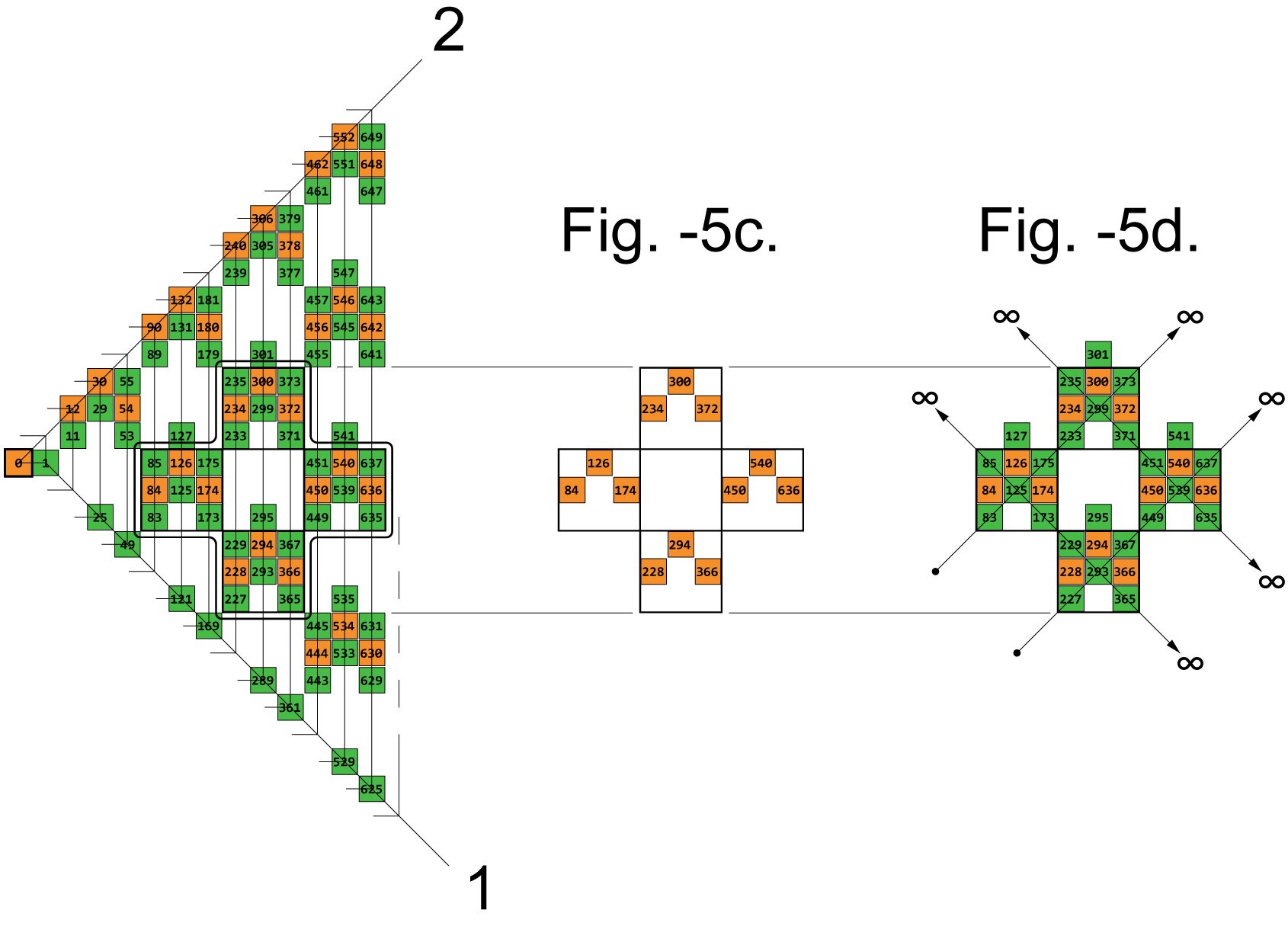Fig. -5.
(From
previous
page.)
Partial View -1.
(Fig.-5.)
In Partial View 1:
A square box has been delineated and
shown again in Fig’s. -5a & -5b.
• Fig. 5a shows
a typical triad with its 90° angle indicated.
• Fig. -5b shows
all the adjacents of that triad.
As can be seen:
• The 90° angle of the triad forces the
5 adjacents in the box to become arranged in
2 rows of numbers with
1 row oriented along each diagonal direction.
Each row extends from box-corner to box-corner.
See arrows.
• The 90° angle of the triad forces
1 adjacent to be located outside the box
and thus to become an isolate.
When this configuration is
positioned over
sector lines -2, -3, -4,
-including the spiral origin-
one or two of the adjacents
will be located differently
to comply with
the 90°angles of the spiral.
See in Fig. -5 at top of page.
Partial View -2.
(Fig.-5.)
In Partial View -2:
4 such boxes
-arranged like checkerboard squares of a single color-
have been delineated and
shown again in Fig’s. -5c & -5d.
These boxes
contact each other,
corner to corner, in both diagonal directions.
Therefore the co-linear rows inside these boxes also
contact each other,
corner to corner, in both diagonal directions.
Thru such contact the co-linear rows join to become
longer rows containing 6 adjacents.
Thru such contact among all the boxes in the spiral
these rows grow indefinitely,
along both diagonal directions, without interruptions.
See arrows.