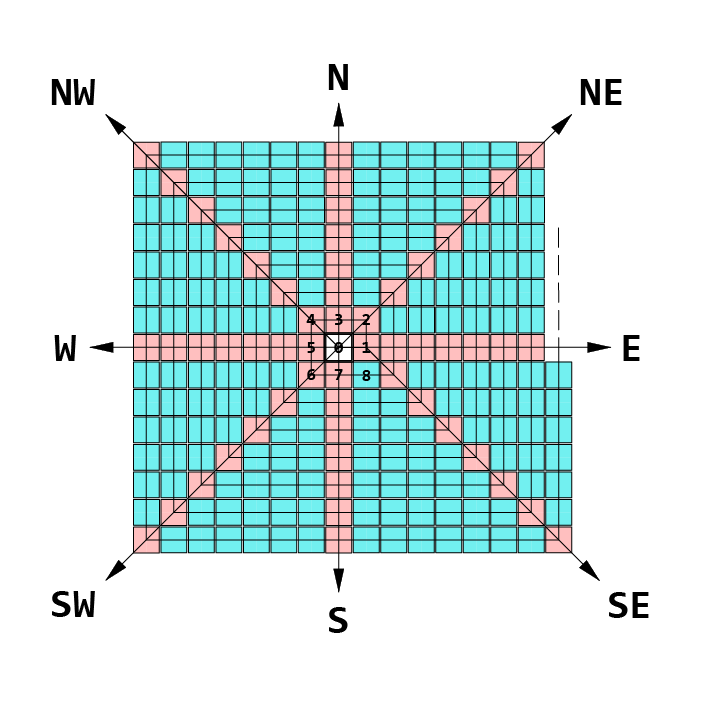
Fig. -1.
Fig. -1 shows an Ulam Spiral
and highlighted therein
8 rows of numbers color-coded red.
These rows can eachly be identified
in convenient cartographic fashion as:
“E” -row, starting at 1,
“NE” -row, starting at 2,
“N” -row, starting at 3,
“NW” -row, starting at 4,
“W” -row, starting at 5,
“SW” -row, starting at 6,
“S” -row, starting at 7,
“SE” -row, starting at 1.
Given the geometric prominence
of these rows in the spiral they can be
referred to as the “cardinal rows”.
Interspersed among these rows are
8 triangular areas of numbers, color-coded blue.
These areas can eachly be identified
in convenient cartographic fashion as:
“E/NE” -area,
“N/NE” -area,
“N/NW” -area,
“W/NW” -area,
“W/SW” -area,
“S/SW” -area,
“S/SE” -area,
“E/SE” -area.
These areas can be referred to as
the “inter-areas”.
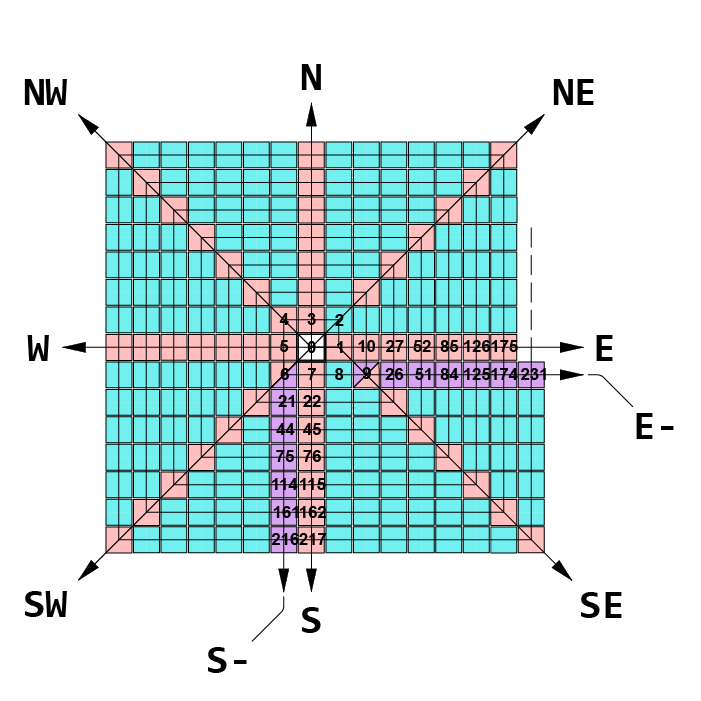
Fig. -2.
spiral origin at 0.
Note -1.
Fig. -2 shows
the spiral with its origin at 0.
As can be seen, it does not have any
prime adjacent on any of the cardinal rows,
except for:
1 at the start of the “E” -row,
5 at the start of the “W” -row,
7 at the start of the “S” -ow.
All the other prime adjacent are
located in the inter-areas.
This remains true even as
the spiral grows to infinity.
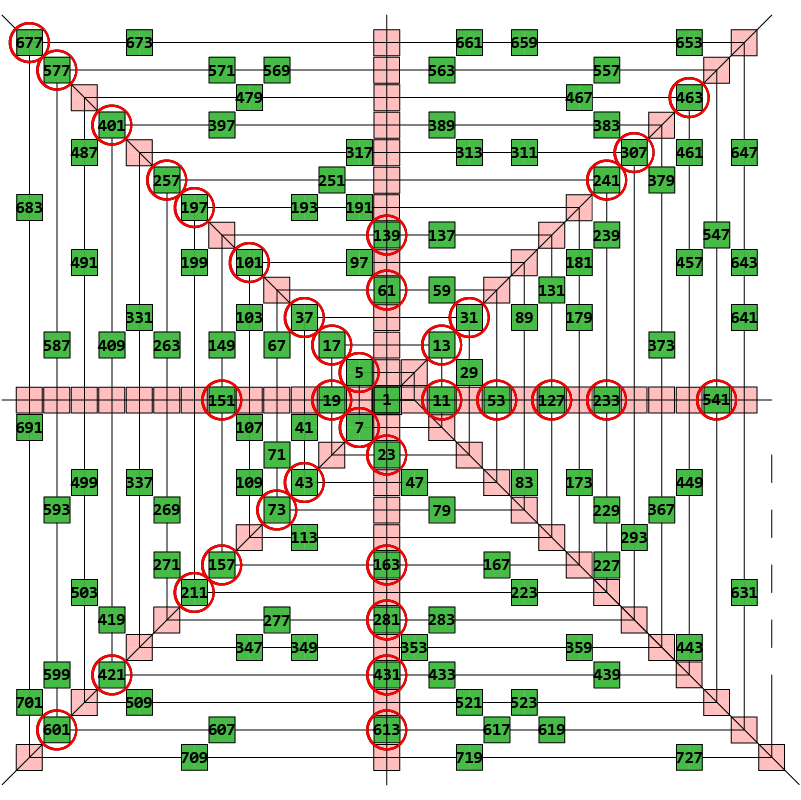
Fig. -3.
spiral origin at 1.
Note -2.
Fig. -3 shows
the spiral with its origin at 1.
as can be seen, it has
prime adjacent located on
all the cardinal rows
except the “SE” -row.
These prime adjacent are
indicated by the red circles.
Note -3.
From comparing the situations described in
Notes -1 & -2 one must conclude that
the Ulam Spiral with origin at 0
is vastly superior to
the Ulam Spiral with origin at 1.
This because of the
higher state of organization manifest in the latter,
where all the prime adjacents -except 1, 5, 7,- are
cleared from the cardinal rows and
herded into the inter-areas.
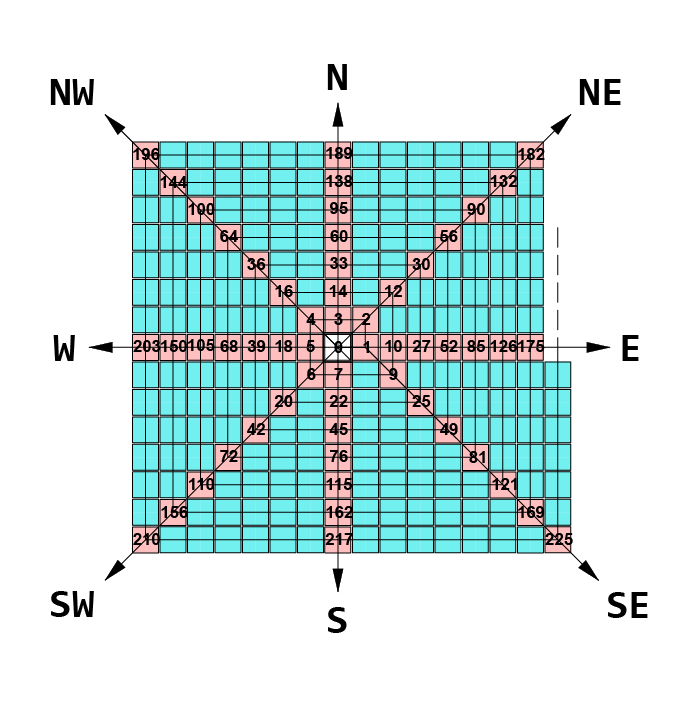
Fig. -4.
In Fig. -4:
The “E” -row consists of the following numbers:
1, 10, 27, 52, 85, 126,175, … definable as:
n(4n – 3), 1 ≤ n < ∞.
The “NE” -row consists of the following numbers:
2, 12, 30, 56, 90, 132, 182, … definable as:
(2n + 1)(2n + 2), 0 ≤ n < ∞
The “N” -row consists of the following numbers:
3, 14, 33, 60, 95, 138, 189, … definable as:
n(4n – 1), 1 ≤ n < ∞
The “NW” -row consists of the following numbers:
4, 16, 36, 64, 100, 144, 196, … definable as:
(2n)^2, 1 ≤ n < ∞
The “W” -row consists of the following numbers:
5, 18, 39, 68, 105, 150, 203, … definable as:
n(4n + 1), 1 ≤ n < ∞
The “SW” row consists of the following numbers:
6, 20, 42, 72, 110, 156, 210, … definable as:
2n(2n + 1), 1 ≤ n < ∞
The “S” -row consists of the following numbers:
7, 22, 45, 76, 115, 162, 217, … definable as:
n(4n + 3), 1 ≤ n < ∞
The “SE” -row consists of the following numbers:
1, 9, 25, 49, 81, 121, 169, 225, … definable as:
(2n + 1)^2, 0 ≤ n < ∞
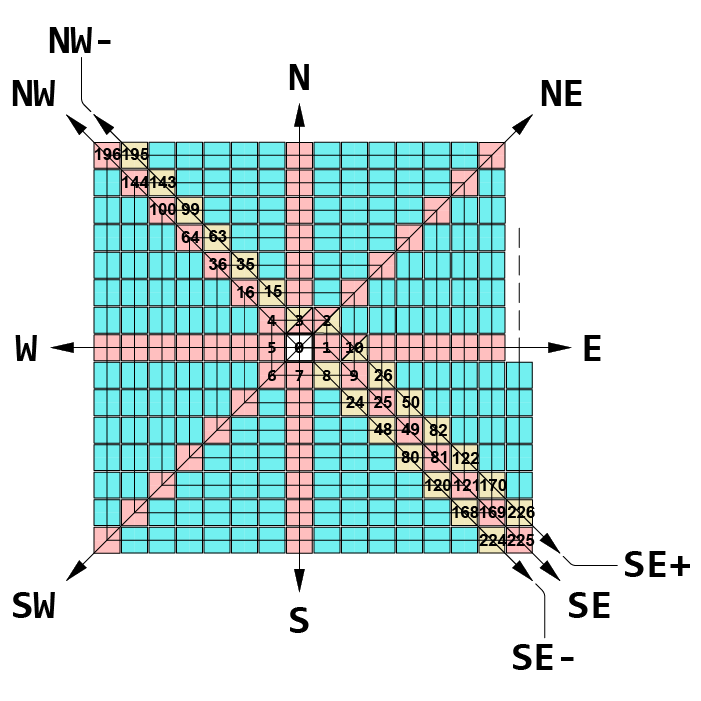
In Fig. -5:
Adjacent to the “SE” -row, to its left,
there is another row, starting at 8,
whose numbers consist of
numbers from the “SE” -row, eachly decreased by 1.
That row can be defined as the “SE-” -row.
Adjacent to the “SE” -row, to its right,
there is another row, starting at 2,
whose numbers consist of
numbers from the “SE” -row, eachly increased by 1.
That row can be defined as the “SE+” -row.
Adjacent to the “NW” -row, to its right,
there is another row, starting at 3,
whose numbers consist of
numbers from the “NW” -row, eachly decreased by 1.
That row can be defined as the “NW-” -row.
These 3 rows are color-coded yellow.
The “SE-” -row consists of the following numbers:
8, 24, 48, 80, 120, 168, 224, … definable as:
(2n + 1)^2 – 1, 1 ≤ n < ∞.
The “SE+” -row consists of the following numbers:
2, 10, 26, 50, 82, 122,170, 226, … definable as:
(2n + 1)^2 + 1, 1 ≤ n < ∞.
The “NW” -row consists of the following numbers:
3, 15, 35, 63, 99, 143,195, … definable as:
(2n)^2 – 1, 1 ≤ n < ∞.
The spiral does not
have any prime adjacent
on these 3 added rows.
This remains true even as
the spiral grows to infinity.
In Fig. -6:
Adjacent to the “S” -row, to its left,
there is another row, starting at 6,
whose numbers consist of
numbers from the “S” -row, eachly decreased by 1.
That row can be identified as the “S-” -row.
Adjacent to the “E” -row, below it,
there is another row, starting at 9,
whose numbers consist of
numbers from the “E” -row, eachly decreased by 1.
That row can be identified as the “E-” -row.
These numbers are color-coded purple.
The “S-” -row consists of the following numbers:
6, 21,44, 75,114, 161, 216, … definable as:
(n + 2)(4n + 3), 0 ≤ n < ∞.
The “E-” -row consists of the following numbers:
9, 26, 51, 84, 125, 174, 231, … definable as:
n(4n + 5), 1 ≤ n < ∞.
The spiral does not
have any prime adjacents
on these 2 added rows.
This remains true even as
the spiral grows to infinity.
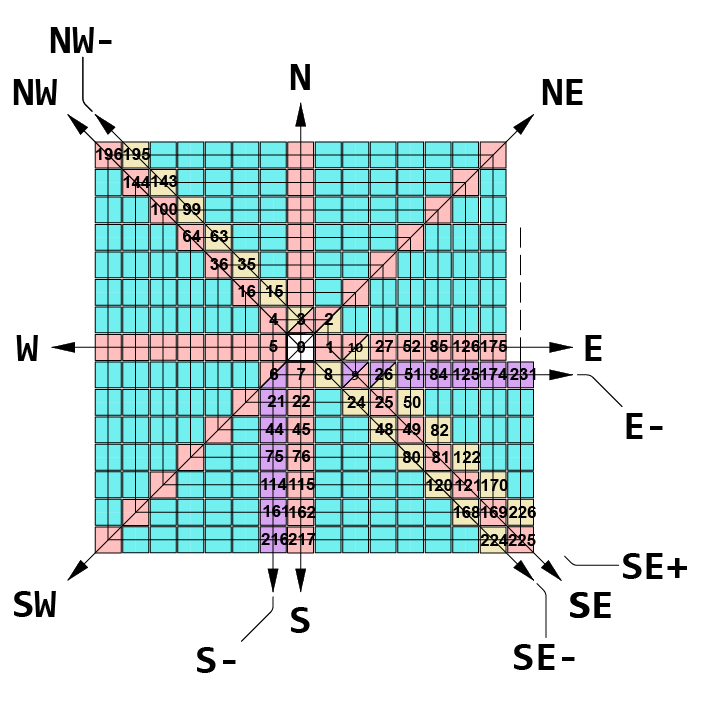
Fig. -7.
In Fig. -7:
the 3 added rows shown in Fig. -5 &
the 2 added rows shown in Fig. -6
are all represented.
These rows obviously diminish
the space available for
the prime adjacents in
some of the inter-areas.
The totality of space available
for the prime adjacents
is shown in Fig. -7,
color-coded blue.