Introduction.
Created by Stanislaw Ulam in 1963, the Ulam Spiral is a
graphical representation of the set of prime numbers.
Ulam Plotted the positive integers on a square spiral and
marked the prime numbers. From this image it was apparent there were
diagonal rows -in both directions- created from what seems like a
disproportionately high number of prime numbers.
As it is human nature to look for patterns mathematicians have spent
decades trying to find any rhyme or reason to this pattern phenomenon.
For some years I’ve thought about the well-known mysteries surrounding
the placement of the prime numbers on that spiral:
• The rows of numbers along the diagonal directions.
• The many different lengths of these rows.
• The many different lengths of the gaps between collinear rows.
All this with the aim of revealing the mathematics governing such placement.
Having seen the mathematics, I simply want to share with others
through the presentation of these in this site,
doing so completely on just this page and the next.
The subsequent interactive page will help to
demonstrate these peculiarities of the spiral.
Pages -4 and -5 contain
advisories pertaining to methods of
populating the spiral in manners that are
most beneficial for exposing internal structures,
with rationales provided.
Also shown:
(6) Tripolar Spiral,
(7) Tetrapolar Spiral,
each featuring remarkably long rows of primes.
In the tripolar spiral the numbers
constituting these rows are located on
every other arc-segment of the spiral.
this situation is true for all polar spirals with
an odd number of poles.
In the tetrapolar spiral the numbers
constituting these rows are located on
every successive arc-segment of the spiral.
this situation is true for all polar spirals with
an even number of poles.
See
(8) Polar Spirals, Operable
for additional polar spirals,
ranging from dipolar through heptapolar.
Detail -A.

The detail above shows
a row of consecutive 6-folds
from “0” thru “120”.
(“0” is a 6-fold because 0 x 6 = 0.)
Det. -B.

The Detail above shows
the row from Det. -A.
Shown below and/or above each 6-fold is an
adjacent prime number, if there is one.
“120” is the 1st. 6-fold
without an adjacent prime number.
Det.-C.

The Detail above shows
the row from Det. -A.
Shown below and/or above each 6-fold is an
adjacent composite number, if there is one.
“120” is the 1st. 6-fold
with 2 adjacent composite numbers.
This website continuously discusses
“Numbers adjacent to the 6-folds”.
That’s a lengthy phrase, making it
more convenient to refer to them as
“The adjacent numbers”,
or, in informal shorthand style:
“The adjacents”.
A single such number then is
“An adjacent”,
using the word “adjacent” as a noun.
The Ulam spiral shown below is
populated by prime numbers.
One can clearly see
its well known mysterious features.
(Every prime number -except “2” & “3”-
is an adjacent.)
The Ulam spiral shown below is
populated by composite adjacents,
such as the ones shown in Det. -C.
One can clearly see
that this spiral has the same
mysterious features
as the spiral to the left.
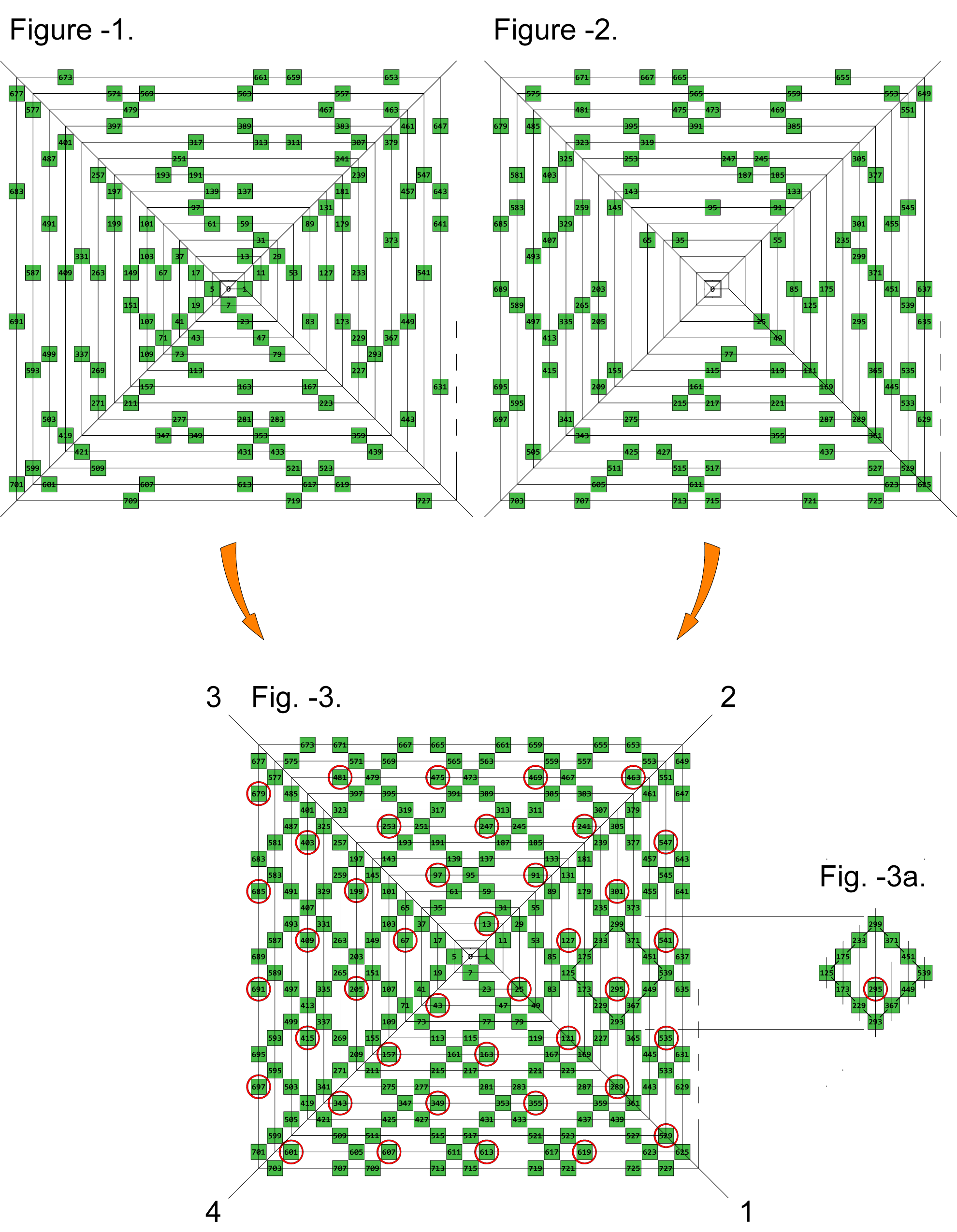
The spiral above shows
the following populations together:
• The prime adjacents of the spiral per Fig. -1.
• The composite adjacents of the spiral per Fig. -2.
As can be seen:
When the spiral is populated by both groups
there are only uninterrupted endless rows
oriented along both diagonal directions.
Some of these rows have a beginning but no end,
others have neither a beginning nor an end.
Interspersed among these rows is
a regular pattern of isolated numbers,
shown circled in red.
They can be prime or composite.
Thus:
• The irregular gaps between the in-line rows
in the spiral per Fig. -1 are caused by
the absence of the composite adjacents.
• The irregular gaps between the in-line rows
in the spiral per Fig. -2 are caused by
the absence of the prime adjacents.
Thus also:
•The orientation of the uninterrupted endless rows
along both diagonal directions
seen in the spiral per Fig. -3
is preserved in the fragments of these rows
seen in the spirals per Fig’s. -1 & -2.
(The cause for the diagonal directions
of the rows in the spiral per Fig. -3
will be shown on the next page.)
To summarize:
The mysteries associated with the
spirals per Fig’s. -1 & -2 exist only because
the set of prime adjacents by themselves and
the set of composite adjacents by themselves
are ‘incomplete’, being mere subsets of the
complete set comprised of all adjacents.
In the spiral per Fig. -3
any pair of adjacent parallel rows
-along both diagonal directions-
have the same interspace, thus forming
a pattern of squares,
such as the one shown in Fig. -3a.
Each of these squares contain
an isolated number in one of its corners
shown circled in red in Fig. -3a.
These numbers can be conveniently called
“The isolated ones”, or, informally,
“The isolates”.
Fig. -4.

Fig. -4 shows the spiral
populated exclusively by the 6-folds.
As can be seen:
the 6-folds are grouped in
regularly spaced 90° V-shaped clusters
each consisting of 3 numbers.
These 3-number clusters can be
called “Triads”.
Fig. -5.

Fig. -5 shows the spiral per Fig. -4
additionally populated by
all the adjacents, clearly showing
the manner of their adjacency.
Note that, generally:
the void areas
have the same peripheries as
the filled areas.
